miércoles, 4 de noviembre de 2015

TEOREMA DE BERNOULLI

APLICACIONES DEL TEOREMA DE BERNOULLI JUNTO CON EL TUBO DE VENTURI.-
La utilización de un tubo de Venturí en el carburador de un automóvil , es un ejemplo familiar del teorema de Bernoulli. La presión del aire, que pasa a través del cuerpo del carburador, disminuye cuando pasa por un estrangulamiento. La disminución de presión permite que fluya la gasolina, se vaporice y se mezcle con la corriente de aire.
·         TUBO DE VENTURI
Un venturi es un dispositivo que clasicamente incorpora una simple convergencia y divergencia a travez de una sección y usa los principios de Bernoulli para relacionar la velocidad con la presión del fluido. Este principio se basa en que cuando el gas o liquido en movimiento, baja su presión y aumenta su velocidad.
Un tubo de venturi es usado para medir la velocidad del flujo de un fluido. En la garganta, el area es reducida de A1 a A2 y su velocidad se incrementa de V1 a V2. En el punto 2, donde la velocidad es máxima, la presión es mínima. Esto lo sabemos de la ecuación de Bernoulli.
Este dispositivo se utiliza para medir el gasto de una tubería. Al escurrir el fluido de la tubería a la garganta, la velocidad aumenta notablemente, y en concecuencia, la presión dismiuye; el gasto transportado por la tubería en el caso de un flujo incompresible esta en función de la lectura del manómetro.
Las presiones en la seccion 1 y en la garganta (sección 2) son presiones reales, en tanto que las velocidades correspondientes obtenidas en la ecuación de Bernoulli sin un término de pérdidas son velocidades teóricas. Si se consideran las pérdidas en la ecuación de la energía entonces se trata de velocidades reales. En lo que sigue se obtendrá primero la velocidad teórica en la garganta al aplicar la ecuación de Bernoulli sin el término de pérdidas. Multiplicando este valor por el coeficiente Cv, se determinará la velocidad real. Esta última, multiplicada por el área real de la garganta, permite obtener el gasto que circula por la tubería.
Nota: Para obtener resultados precisos, el tubo de Venturi debe estar precedido por una longitud de al menos diez veces en diametro de la tubería.
Donde V1, V2, p1 y p2 son las velocidades y presiones en las secciones 1 y 2 respectivamente. Esta ecuación incorpora la concervación de la energía para fluidos.
Usaremos la ecuación de continuidad para flujo de fluidos. Esta se basa en que con ausencia de pérdida de masa, el flujo de fluido que entra en una región dada debe ser igual al que sale.
Para flujo incompresible:
Juntando la ecuación de Bernoulli con la de continuidad, se tendrá:
Por otro lado la diferencia manométrica h se puede relacionar con la diferencia de presiones al escribir la ecuación del manómetro. De este modo se obtiene una expresión para el gasto.
Donde S0 es la gravedad específica del liquido en el manómetro y S1 es la gravedad específica del líquido a travez de la tubería. Esta expresión que constituye la ecuación del tubo de venturi para flujo incompresible. El gasto depende de la diferencia manométrica h. 
El coeficiente Cv se determina mediante un método de calibración (número de Reynolds).


Cuándo la velocidad de un fluido en cualquier punto dado permanece constante en el transcurso del tiempo, se dice que el movimiento del fluido es uniforme. Esto es, en un punto dado cualquiera, en un flujo de régimen estable la velocidad de cada partícula de fluido que pasa es siempre la misma. En cualquier otro punto puede pasar una partícula con una velocidad diferente, pero toda partícula que pase por este segundo punto se comporta allí de la misma manera que se comportaba la primera partícula cuando pasó por este punto. Estas condiciones se pueden conseguir cuando la velocidad del flujo es reducida. Por otro lado, en un flujo de régimen variable, las velocidades son función del tiempo. En el caso de un flujo turbulento, las velocidades varían desordenadamente tanto de un punto a otro como de un momento a otro.
La dinámica de los líquidos, está regida por el mismo principio de la conservación de la energía, el cual fue aplicado a ellos por el físico suizo Daniel Bernoulli (1700-1782), obteniendo como resultado una ecuación muy útil en este estudio, que se conoce con su nombre.
Para ello se puede considerar los puntos 1 y 2, de un fluido en movimiento, determinando la energía mecánica de una porción de éste, a lo largo del filete de fluido en movimiento que los une
La dinámica de los líquidos, está regida por el mismo principio de la conservación de la energía, el cual fue aplicado a ellos por el físico suizo Daniel Bernoulli (1700-1782), obteniendo como resultado una ecuación muy útil en este estudio, que se conoce con su nombre.

Para ello se puede considerar los puntos 1 y 2, de un fluido en movimiento, determinando la energía mecánica de una porción de éste, a lo largo del filete de fluido en movimiento que los une.
El principio de Bernoulli, también denominado ecuación de Bernoulli o trinomio de Bernoulli, describe el comportamiento de un fluido moviéndose a lo largo de una corriente de agua. Fue expuesto por Daniel Bernoulli en su obra Hidrodinámica (1737) y expresa que en un fluido ideal (sin viscosidad ni rozamiento) en régimen de circulación por un conducto cerrado, la energía que posee el fluido permanece constante a lo largo de su recorrido.

La ecuación de Bernoulli

La energía de un fluido en cualquier momento consta de tres componentes:

  • cinética: es la energía debida a la velocidad que posea el fluido;
  • potencial o gravitacional: es la energía debido a la altitud que un fluido posea;
  • energía de presión: es la energía que un fluido contiene debido a la presión que posee.
La siguiente ecuación conocida como "ecuación de Bernoulli" (trinomio de Bernoulli) consta de estos mismos términos.
\frac{V^2 \rho}{2}+{P}+{\rho g z}= \text{constante}
donde:
Para aplicar la ecuación se deben realizar los siguientes supuestos:
  • Viscosidad (fricción interna) = 0 Es decir, se considera que la línea de corriente sobre la cual se aplica se encuentra en una zona 'no viscosa' del fluido.
  • Caudal constante
  • Flujo incompresible, donde ρ es constante.
  • La ecuación se aplica a lo largo de una línea de corriente o en un flujo laminar.
Aunque el nombre de la ecuación se debe a Bernoulli, la forma arriba expuesta fue presentada en primer lugar por Leonhard Euler.
Un ejemplo de aplicación del principio se da en el flujo de agua en tubería.
\overbrace{{V^2 \over 2 g}}^{\mbox{cabezal de velocidad}}+\overbrace{\underbrace{\frac{P}{\gamma}}_{\mbox{cabezal de presión}} + z}^{\mbox{altura o carga piezométrica}} = \overbrace{H}^{\mbox{Cabezal o Altura hidráulica}}
También se puede reescribir este principio en forma de suma de presiones multiplicando toda la ecuación por \gamma, de esta forma el término relativo a la velocidad se llamará presión dinámica, los términos de presión y altura se agrupan en la presión estática.
Esquema del efecto Venturi.
\underbrace{\frac{\rho V^2}{2}}_{\mbox{presión dinámica}}+\overbrace{P+ \gamma z}^{\mbox{presión estática}}=\text{constante}
o escrita de otra manera más sencilla:
q+p=p_0
donde
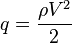
  • q=\frac{\rho V^2}{2}
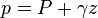
  • p=P+ \gamma z
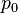  • p_0 es una constante-
Igualmente podemos escribir la misma ecuación como la suma de la energía cinética, la energía de flujo y laenergía potencial gravitatoria por unidad de masa:
\overbrace{\frac{{V}^2}{2}}^{\mbox{energía cinética}}+\underbrace{\frac{P}{\rho}}_{\mbox{energía de flujo}}+\overbrace{g z}^{\mbox{energía potencial}} = \text{constante}
En una línea de corriente cada tipo de energía puede subir o disminuir en virtud de la disminución o el aumento de las otras dos. Pese a que el principio de Bernoulli puede ser visto como otra forma de la ley de laconservación de la energía realmente se deriva de la conservación de la Cantidad de movimiento.
Esta ecuación permite explicar fenómenos como el efecto Venturi, ya que la aceleración de cualquier fluido en un camino equipotencial (con igual energía potencial) implicaría una disminución de la presión. Este efecto explica porqué las cosas ligeras muchas veces tienden a salirse de un automóvil en movimiento cuando se abren las ventanas. La presión del aire es menor fuera debido a que está en movimiento respecto a aquél que se encuentra dentro, donde la presión es necesariamente mayor. De forma, aparentemente, contradictoria el aire entra al vehículo pero esto ocurre por fenómenos de turbulencia y capa límite.

Ecuación de Bernoulli con fricción y trabajo externo

La ecuación de Bernoulli es aplicable a fluidos no viscosos, incompresibles en los que no existe aportación de trabajo exterior, por ejemplo mediante una bomba, ni extracción de trabajo exterior, por ejemplo mediante una turbina. De todas formas, a partir de la conservación de la Cantidad de movimiento para fluidos incompresibles se puede escribir una forma más general que tiene en cuenta fricción y trabajo:
\frac{{V_1}^2}{2 g}+\frac{P_1}{\gamma}+z_1 + W = h_f + \frac{{V_2}^2}{2 g}+\frac{P_2}{\gamma}+z_2
donde:
  • \gamma es el peso específico (\gamma=\rho g). Este valor se asume constante a través del recorrido al ser un fluido incompresible.
  • W trabajo externo que se le suministra (+) o extrae al fluido (-) por unidad de caudal másico a través del recorrido del fluido.
  • h_f disipación por fricción a través del recorrido del fluido.
  • Los subíndices 1 y 2 indican si los valores están dados para el comienzo o el final del volumen de control respectivamente.
  • g = 9,81 m/s2.

Aplicaciones del principio de Bernoulli

Chimenea
Las chimeneas son altas para aprovechar que la velocidad del viento es más constante y elevada a mayores alturas. Cuanto más rápidamente sopla el viento sobre la boca de una chimenea, más baja es la presión y mayor es la diferencia de presión entre la base y la boca de la chimenea, en consecuencia, los gases de combustión se extraen mejor.

Tubería
La ecuación de Bernoulli y la ecuación de continuidad también nos dicen que si reducimos el área transversal de una tubería para que aumente la velocidad del fluido que pasa por ella, se reducirá la presión.

Natación
La aplicación dentro de este deporte se ve reflejado directamente cuando las manos del nadador cortan el agua generando una menor presión y mayor propulsión.

Carburador de automóvil
En un carburador de automóvil, la presión del aire que pasa a través del cuerpo del carburador, disminuye cuando pasa por un estrangulamiento. Al disminuir la presión, la gasolina fluye, se vaporiza y se mezcla con la corriente de aire.

Flujo de fluido desde un tanque
La tasa de flujo está dada por la ecuación de Bernoulli.

Dispositivos de Venturi
En oxigenoterapia, la mayor parte de sistemas de suministro de débito alto utilizan dispositivos de tipo Venturi, el cual está basado en el principio de Bernoulli.

Aviación
Erróneamente, se ha atribuido el vuelo de los aviones a tener el extradós (parte superior del ala o plano) más curvado que el intradós (parte inferior del ala o plano), causando que la masa superior de aire, al aumentar su velocidad, disminuya su presión, creando así una succión que sustenta la aeronave. Algunas consecuencias de este error, serían que los aviones caerían como plomo contra el suelo al realizar vuelos invertidos, el ángulo de ataque (ángulo entre el eje perpendicular al suelo y las alas de la avión) sería irrelevante, hecho que conocemos falso, pues el ángulo de ataque es decisivo en el vuelo, y además, no serían posibles los vuelos de modelos primitivos como el Curtis 1911 model D type IV pusher. Lo cierto es que el principio de Bernoulli solo es relevante si no hay flotación. El principio en el que se basa el vuelo de los aviones es la tercera ley de Newton, pues las alas de los aviones llegan a desplazar toneladas de aire hacia abajo al alcanzar velocidades altas, produciendo como consecuencia una fuerza de empuje vertical y una aceleración.


Publicadas por a la/s

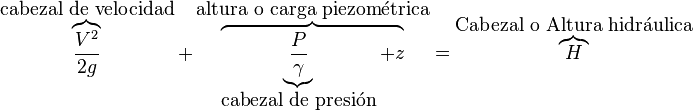
No hay comentarios.:

Publicar un comentario

Suscribirse a: Comentarios de la entrada (Atom)