La ecuación de continuidad es un importante principio
físico muy útil para la descripción de los fenómenos en los que participan
fluidos en movimiento, es decir en lahidrodinámica. Para la formulación
de la ecuación de continuidad de los fluidos se asumen un grupo de
consideraciones ideales que no siempre se tienen en los fenómenos reales de
movimientos de fluidos, de modo que en general, aunque la ecuación es clave
para la interpretación de los fenómenos reales, los cálculos derivados de su
uso serán siempre una aproximación a la realidad, sin embargo, en una buena
parte de los casos con suficiente exactitud como para poder ser considerados
como ciertos.
Antes de entrar en el tema que nos ocupa
debemos definir algunos conceptos importantes y útiles para la comprensión:
1.- Lineas de corriente: Para muchas aplicaciones resulta conveniente
considerar el flujo total del fluido en movimiento como un manojo de corrientes
muy finas (infinitesimales) que fluyen paralelas. Estas corrientes, que
recuerdan hilos, se conocen como lineas de corriente.2.-
Flujo laminar: Cuando las lineas de corriente de un flujo nunca se
cruzan y siempre marchan paralelas se le llama flujo laminar. En el
flujo laminar siempre las lineas de corriente marchan en la misma dirección que
la velocidad del flujo en ese punto.3.-
Flujo turbulento: En el flujo
turbulento el movimiento del fluido se torna irregular, las lineas de corriente
pueden cruzarse y se producen cambios en la magnitud y dirección de la
velocidad de estas.4.- Viscosidad: Este término se utiliza
para caracterizar el grado de rozamiento interno de un fluido y está asociado
con la resistencia entre dos capas adyacentes del fluido que se mueven una
respecto a la otra.Entrando en la ecuación de continuidad
La ecuación de continuidad parte de las bases ideales siguientes:
1.- El fluido es incompresible.2.- La temperatura del
fluido no cambia.
3.- El flujo es continuo, es decir su velocidad y
presión no dependen del tiempo.4.- El flujo es
laminar. No turbulento.5.- No existe
rotación dentro de la masa del fluido, es un flujo irrotacional.6.- No
existen pérdidas por rozamiento en el fluido, es decir no hay viscosidad.
|
|
|
Figura 1. Un fluido en movimiento con las lineas
de corriente a lo largo de un tubo imaginario de sección variable.
|
Tomemos un tubo imaginario de sección variable formado por un racimo de
lineas de corriente del interior de un fluido en movimiento como se muestra en
la figura 1. En un intervalo pequeño de tiempo Δt, el fluido que
entra por el fondo del tubo imaginario recorre una distancia Δx1 = v1 Δt siendo v1 la
velocidad del fluido en esa zona. Si A1 es el área de la
sección transversal de esta región, entonces la masa de fluido contenida en la
parte azul del fondo es ΔM1 = ρ1A1 Δx1 = ρ1A1v1Δt, donde ρ es
la densidad del fluido. De la misma forma el flujo que sale por el extremo
superior del tubo imaginario en el mismo tiempo Δt tiene la
masa ΔM2 = ρ2A2v2Δt.
Como la masa debe conservarse y debido también a que el flujo es laminar, la
masa que fluye a través del fondo del tubo en la sección A1,
en el tiempo Δt, será igual a la que fluye en el mismo tiempo
a través de A2. Por lo tanto ΔM1 = ΔM2,
o:
ρ1A1v1Δt = ρ2A2v2Δt
(ecuación 1)
Si dividimos por Δt tenemos que:
ρ1A1v1 = ρ2A2v2
(ecuación 2)
La ecuación 2 se conoce como ecuación
de continuidad.
Como hemos considerado que el fluido es
incompresible entonces ρ1 = ρ2 y
la ecuación de continuidad se reduce a:
A1v1 = A2v2
Es decir, el área de la sección transversal de
un tubo, multiplicada por la velocidad del fluido es constante a todo lo largo
del tubo. El producto Av, que tiene las dimensiones de volumen por
unidad de tiempo se conoce como caudal
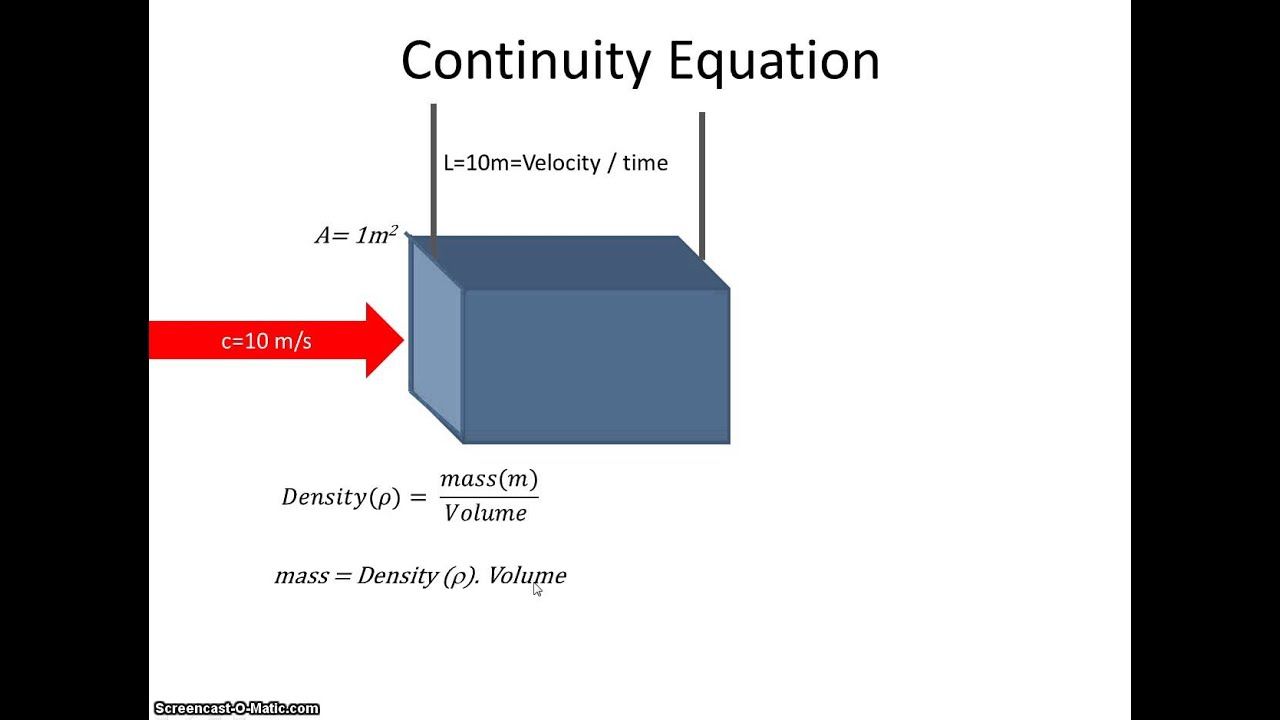
En física, una ecuación de continuidad expresa una ley de conservación de forma matemática, ya sea de formaintegral como de forma diferencial.
En teoría electromagnética, la ecuación de continuidad viene derivada de dos de las ecuaciones de Maxwell. Establece que la divergencia de la densidad de corriente es igual al negativo de la derivada de la densidad de carga respecto del tiempo:
En otras palabras, sólo podrá haber un flujo de corriente si la cantidad de carga varía con el paso del tiempo, ya que esta disminuye o aumenta en proporción a la carga que es usada para alimentar dicha corriente.
Esta ecuación establece la conservación de la carga.
Mecánica de fluidos
En mecánica de fluidos, una ecuación de continuidad es una ecuación de conservación de la masa. Su forma diferencial es:
Mecánica cuántica
En Mecánica cuántica, una ecuación de continuidad es una ecuación de conservación de la probabilidad. Su forma diferencial es:1
Donde  es la densidad de probabilidad de la función de ondas y
es la densidad de probabilidad de la función de ondas y 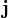 es la corriente de probabilidad o densidad de corriente. Estas dos expresiones se pueden relacionar con la función de onda de una partícula como:
es la corriente de probabilidad o densidad de corriente. Estas dos expresiones se pueden relacionar con la función de onda de una partícula como:
 es la densidad de probabilidad de la función de ondas y
es la densidad de probabilidad de la función de ondas y 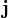 es la corriente de probabilidad o densidad de corriente. Estas dos expresiones se pueden relacionar con la función de onda de una partícula como:
es la corriente de probabilidad o densidad de corriente. Estas dos expresiones se pueden relacionar con la función de onda de una partícula como:Mecánica relativista
En la teoría especial de la relatividad, una ecuación de continuidad debe escribirse en forma covariante, por lo que la ecuación de continuidad usual para la carga eléctrica y otras magnitudes conservadas se suele escribir en teoría de la relatividad como:
La ecuación de continuidad para la densidad másica (o más exactamente la energía másica) y la densidad de momento lineal se escribe en términos del tensor energía impulso:
En el contexto de la teoría general de la relatividad las derivadas parciales deben substituirse por derivadas covariantes:
Donde 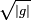 es la raíz del determinante del tensor métrico asociado a las coordenadas
es la raíz del determinante del tensor métrico asociado a las coordenadas  . Y análogamente para la conservación de la energía:
. Y análogamente para la conservación de la energía:
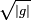 es la raíz del determinante del tensor métrico asociado a las coordenadas
es la raíz del determinante del tensor métrico asociado a las coordenadas  . Y análogamente para la conservación de la energía:
. Y análogamente para la conservación de la energía:
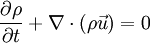
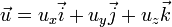 la velocidad del fluido. Es una de las tres
la velocidad del fluido. Es una de las tres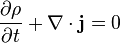

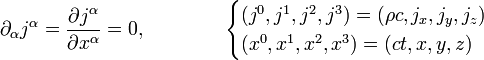
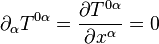
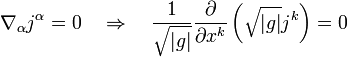
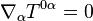
No hay comentarios.:
Publicar un comentario