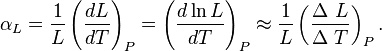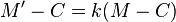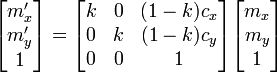Concepto de dilatación
La
dilatación en Física es el aumento de un cuerpo en su volumen, éste se hace más
grande (más largo o ancho, o ambas cosas).La dilatación puede ocurrir por una
variación de temperatura a
presión constante. Esto se conoce como dilatación térmica. Cuando un cuerpo
sólido (sobre todo plano) se calienta, se dilata en largo y ancho aumentando su superficie, pues el
calor otorga a sus moléculas energía, lo que las
hace vibrar intensamente, necesitando entre ellas un espacio mayor. El
coeficiente medio de dilatación superficial es el aumento de su unidad de
superficie, al aumentar su temperatura en un grado. La letra griega gamma es la
que lo representa. La dilatación lineal (aumento de longitud) en un
cuerpo alargado, es proporcional al aumento de temperatura en pequeños
intervalos La dilatación de los gases es mucho mayor que la que sufren los
líquidos o los sólidos
El agua
presenta particularidades en su dilatación, pues al solidificarse, aumenta su
volumen y disminuye su densidad. Cuando alcanza los 10 º C se equipara con
otros fluidos su curva de dilatación.En Biología se conoce como dilatación de
las pupilas, a cuando éstas se agrandan, ya sea por la falta de luz o a consecuencia de
emociones, medicamentos o
drogas, actuando sobre ellas el sistema nervioso simpático.
El término dilatación puede referirse:
- a una dilatación térmica, un proceso físico por el cual se producen cambios de volumen como resultado de cambios de temperatura;
- a una transformación dilatación u homotecia en un espacio euclídeo;
- a una dilatación, un proceso fisiológico que ocurre durante el parto. Se denomina dilatación térmica al aumento de longitud, volumen o alguna otra dimensión métrica que sufre un cuerpo físico debido alaumento de temperatura que se provoca en él por cualquier medio. La contracción térmica es la disminución de propiedades métricas por disminución de la misma.
Dilatación lineal
Es aquella en la cual predomina la variación en una única dimensión, o sea, en el ancho, largo o altura del cuerpo. El coeficiente de dilatación lineal, designado por αL, para una dimensión lineal cualquiera, se puede medir experimentalmente comparando el valor de dicha magnitud antes y después:Donde , es el incremento de su integridad física cuando se aplica un pequeño cambio global y uniforme de temperatura
, es el incremento de su integridad física cuando se aplica un pequeño cambio global y uniforme de temperatura 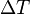 a todo el cuerpo. El cambio total de longitud de la dimensión lineal que se considere, puede despejarse de la ecuación anterior:
a todo el cuerpo. El cambio total de longitud de la dimensión lineal que se considere, puede despejarse de la ecuación anterior:![L_f = L_0 [1 +\alpha_L (T_f - T_0)]\;](https://upload.wikimedia.org/math/4/d/8/4d8d9e521d59aa36de0d776706db3b16.png) Donde:
Donde:- α=coeficiente de dilatación lineal [°C-1]
- L0 = Longitud inicial
- Lf = Longitud final
- T0 = Temperatura inicial.
- Tf = Temperatura final
Dilatación volumétrica
Es el coeficiente de dilatación volumétrico, designado por αV, se mide experimentalmente comparando el valor del volumen total de un cuerpo antes y después de cierto cambio de temperatura como, y se encuentra que en primera aproximación viene dado por: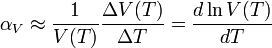 Experimentalmente se encuentra que un sólido isótropo tiene un coeficiente de dilatación volumétrico que es aproximadamente tres veces el coeficiente de dilatación lineal. Esto puede probarse a partir de la teoría de la elasticidad lineal. Por ejemplo si se considera un pequeño prisma rectangular (de dimensiones: Lx, Ly y Lz), y se somete a un incremento uniforme de temperatura, el cambio de volumen vendrá dado por el cambio de dimensiones lineales en cada dirección:
Experimentalmente se encuentra que un sólido isótropo tiene un coeficiente de dilatación volumétrico que es aproximadamente tres veces el coeficiente de dilatación lineal. Esto puede probarse a partir de la teoría de la elasticidad lineal. Por ejemplo si se considera un pequeño prisma rectangular (de dimensiones: Lx, Ly y Lz), y se somete a un incremento uniforme de temperatura, el cambio de volumen vendrá dado por el cambio de dimensiones lineales en cada dirección: Esta última relación prueba que
Esta última relación prueba que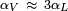 , es decir, el coeficiente de dilatación volumétrico es numéricamente unas 3 veces el coeficiente de dilatación lineal de una barra del mismo material.
, es decir, el coeficiente de dilatación volumétrico es numéricamente unas 3 veces el coeficiente de dilatación lineal de una barra del mismo material.Dilatación de área
Cuando un área o superficie se dilata, lo hace incrementando sus dimensiones en la misma proporción. Por ejemplo, una lámina metálica aumenta su largo y ancho, lo que significa un incremento de área. La dilatación de área se diferencia de la dilatación lineal porque implica un incremento de área.El coeficiente de dilatación de área es el incremento de área que experimenta un cuerpo de determinada sustancia, de área igual a la unidad, al elevarse su temperatura un grado centígrado. Este coeficiente se representa con la letra griega gamma (γ). El coeficiente de dilatación de área se usa para los sólidos. Si se conoce el coeficiente de dilatación lineal de un sólido, su coeficiente de dilatación de área será dos veces mayor: Al conocer el coeficiente de dilatación de área de un cuerpo sólido se puede calcular el área final que tendrá al variar su temperatura con la siguiente expresión:
Al conocer el coeficiente de dilatación de área de un cuerpo sólido se puede calcular el área final que tendrá al variar su temperatura con la siguiente expresión:![A_f = A_0 [1 +\gamma_A (T_f - T_0)]\;](https://upload.wikimedia.org/math/8/4/4/84444b9c6e865aaf0b6d1376be7a9a6b.png) Donde:
Donde:- γ=coeficiente de dilatación de área [°C-1]
- A0 = Área inicial
- Af = Área final
- T0 = Temperatura inicial.
- Tf = Temperatura final
Causa de la dilatación
En un sólido las moléculas tienen una posición razonablemente fija dentro de él. Cada átomo de la red cristalina vibra sometido a una fuerza asociada a un pozo de potencial, la amplitud del movimiento dentro de dicho pozo dependerá de la energía total de átomo o molécula. Al absorber calor, la energía cinética promedio de las moléculas aumenta y con ella la amplitud media del movimiento vibracional (ya que la energía total será mayor tras la absorción de calor). El efecto combinado de este incremento es lo que da el aumento de volumen del cuerpo.En los gases el fenómeno es diferente, ya que la absorción de calor aumenta la energía cinética media de las moléculas lo cual hace que la presión sobre las paredes del recipiente aumente. El volumen final por tanto dependerá en mucha mayor medida del comportamiento de las paredes.
Homotecia
Una homotecia es una transformación afín que, a partir de un punto fijo, multiplica todas las distancias por un mismo factor. En general una homotecia de razón (λ) diferente de 1 deja un único punto fijo, llamado centro.
Definición
Sea E un espacio vectorial sobre un cuerpo 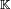 . Sea X un elemento (visto como un punto) de E. La homotecía de centro C y de razón k, denotada
. Sea X un elemento (visto como un punto) de E. La homotecía de centro C y de razón k, denotada 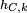 envía un punto M del espacio vectorial sobre el punto M' tal que:
envía un punto M del espacio vectorial sobre el punto M' tal que:
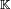 . Sea X un elemento (visto como un punto) de E. La homotecía de centro C y de razón k, denotada
. Sea X un elemento (visto como un punto) de E. La homotecía de centro C y de razón k, denotada 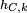 envía un punto M del espacio vectorial sobre el punto M' tal que:
envía un punto M del espacio vectorial sobre el punto M' tal que:(1a)
La ecuación anterior puede escribirse también como una transformación afín de la forma:
(1b)
La anterior relación puede escribirse vectorialmente en el plano como:
Donde: 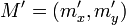 ,
, 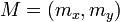 y
y 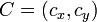 .
.
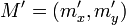 ,
, 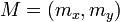 y
y 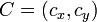 .
.
En tres o más dimensiones la fórmula anterior se generaliza trivialmente.
La homotecia es una transformación afín, composición de una transformación lineal y una traslación, y por consiguiente conserva:
- el alineamiento: las imágenes de puntos alineados son alineados: (A,B,C) y (A', B', C') en la figura
- el centro de un segmento, y más generalmente el baricentro: la imagen del baricentro es el baricentro de las imágenes. En la figura, B es el centro de [A;C] y por lo tanto B' es el de [A';C']
- La imagen de línea es otra línea paralela a la original.
- el paralelismo: dos líneas paralelas tienen imágenes paralelas. En la figura (B'E') // (C'D') porque (BE) //(CD).
- Si k ≠ 1, el centro de la homotecia es el único punto fijo (k = 1 corresponde a la identidad de E: todos los puntos son fijos).
- k = - 1 corresponde a una simetría de centro C.
- Si k ≠ 0,
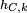 admite como trasformación recíproca
admite como trasformación recíproca  (cuando k = 0, no es biyectiva).
(cuando k = 0, no es biyectiva). - Al componer dos homotecias del mismo centro se obtiene otra homotecia con este centro, cuya razón es el producto de las razones de las homotecias iniciales:
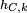 o
o 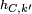 =
= 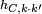 .
. - Al componer homotecias de centros distintos, de razones k y k', se obtiene una homotecia de razón k·k' cuando k·k'≠1, y una traslación si k·k'=1. El conjunto de las homotecias (con k≠0) y las translaciones forman un grupo.
Cuando el cuerpo de escalares son los Reales, se cumple que:
- todas las longitudes son multiplicadas por |k|, el valor absoluto de la razón.
- el cociente de longitudes es conservado: A'C'/B'E' = AC/BE en la figura
- los ángulos orientados son conservados, en particular los ángulos rectos. Es obvio en la figura.
Más aún:
- k = - 1 corresponde a la simetría de centro C que es la rotación alrededor de C de ángulo π radianes(180º).
- |k| > 1 implica una ampliación de la figura.
- |k| < 1 implica una reducción.
- k < 0, la homotecia se puede expresar como la composición de una simetría con una homotecia de razón |k|, ambas de igual centro. Que la homotecia original.
Homotecias en el plano real
En esta sección, los escalares serán números reales.
Una homotecia generalizada en el plano es una transformación del plano en sí mismo en donde una recta y su homóloga son paralelas. De esta definición, se sigue fácilmente que las homotecias conservan ángulos, es decir sontransformaciones conformes del plano, que el conjunto de homotecias forman un 'grupo' y que las traslaciones son casos particulares de las homotecias.
Consideremos la homotecia en la cual la recta OA se transforma en la recta O'B, siendo O' el homólogo de O y B el homólogo de A. Necesariamente, las rectas OO' y AB son invariantes en esta homotecia y el punto H1, centro de la homotecia, es invariante. En esta homotecia la circunferencia de centro O y radio OA se transforma en la circunferencia de centro O' y de radio O'B y la razón de la homotecia es la razón (positiva) de los segmentos O'B y OA.
Si por el contrario, el punto A se transforma en B' entonces la recta AB' es invariante y es el punto H2 el centro de homotecia. En este caso, la razón de la homotecia es negativa.
Ejes de homotecia
Dadas dos circunferencias, éstas siempre se pueden considerar como homotéticas una de la otra.
En la figura de a lado, las líneas de s1, es en la homotecia de razón positiva, con centro en P1, o de razón negativa, con centro de homotecia en N1.
Consideremos las homotecias, una con centro en P1 en la cual la circunferencia S2 es homotética de la circunferencia s1, y la homotecia de centro P3 en la que la circunferencia s3 es homotética a la circunferencia s2. La composición de estas dos homotecias es la homotecia de centro en P2 que transforma la circunferencia s1 en la circunferencia s3. Es por esta razón que los centros de homotecia positivos, P1, P2 y P3 están alineados. En general, dadas tres circunferencias existen seis centros de homotecia, alineados tres a tres sobre cuatro rectas.
Estas rectas son las llamadas ejes de homotecia de las tres circunferencias dadas.