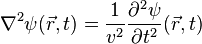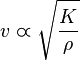Cualquiera que haya sentido vibrar la Tierra durante un terremoto, haya visto la espectacular manifestación de luz, fuego y energía de un volcán, o haya caminado por las laderas y cumbres de una montaña, le es fácil de comprender que la Tierra es un planeta, cuando menos dinámico, lleno de Energía Interna, que vibra, ruge y se estremece, como pueden hacerlo cualquiera de los hijos que viven sobre su piel.
Esa manifestación de la energía interna, ha sido y es uno de los mayores enigmas que los humanos, con ansias de conocimiento, han deseado durante siglos desvelar. Aunque terremotos y volcanes no dejan indiferente a quienes los sienten, la existencia de fósiles de animales marinos en las rocas de las montañas a cientos de kilómetros del mar más próximo, es algo que fascina a quien se toma la molestia de preguntarse su origen.
Las montañas, su origen y formación, han sido y son fuente de fascinación para científicos y amantes de la Naturaleza, constituyen una de las expresiones mas notables de la energía interna de la Tierra. Solsticio de invierno en la Serranía de Ronda.
Nos faltarían dedos en el cuerpo para enumerar las teorías que se han propuesto con el fin de explicar estos fenómenos. Sin embargo, las teorías que se formularon cuando la humanidad empezó a viajar con facilidad por la faz del planeta, se hicieron más coherentes con las observaciones.
La posibilidad de contemplar rocas, fósiles y eventos geológicos iguales en lugares muy alejados del planeta, así como la similitud entre la línea de costa de América del Sur y África, o entre la península Arábiga y el oeste de África, fueron estímulos que fomentaron el planteamiento de teorías atrevidas, como la posibilidad de que los continentes no hayan estado siempre en el lugar que hoy ocupan.
Pero en la ciencia como en la vida el planteamiento de ideas nuevas y rompedoras con las dominantes, suelen generar polémicas, que por desgracia, trasciende el límite de lo científico.
Es normal que las ideas conservadoras e inmovilistas se arraiguen en las mentes de las personas con una posición social o profesional consolidada; como también es normal que las ideas mas arriesgadas sean bandera de la juventud intrépida que debe de hacerse un lugar en su mundo. Las dos fuerzas, conservadoras y revolucionarias, son manifestaciones de las que existen en la naturaleza: por un lado la fuerza del cambio y la evolución; por otro las fuerzas que dan estabilidad y tiempo necesarios para consolidar esos cambios.
Y en la ciencias de la Tierra no pudo ser diferente cuando a principios del siglo pasado el intrépido y arriesgado investigador alemán, Alfred Wegener se le ocurriera oponerse a las teorías dominantes y afirmar que los continentes se mueven y bastante, sobre la faz del planeta.
Su teoría, denominada “Deriva continental”, suponía que los continentes, menos densos, flotaban como iceberg sobre el fondo rocoso de los océanos, más densos. Que debido a las fuerzas gravitatorias del Sol, la Luna y los planetas, y a la centrífuga de rotación de la Tierra, estos se movían “a la deriva”, chocando de vez en cuando entre si, provocando el plegamiento y emersión de los fondos rocosos situado entre ambos, lo que producía la formación de las cordilleras.
Uno de los grandes meritos de Wegener, fue la recopilación de un gran numero de pruebas que avalaban su teoría:
- Existencia e fósiles iguales en continentes separados por océanos, que la nueva teoría de la Isostasiahacia incompatible con la existencia de “puentes intercontinentales”, que a modo de islas, pudieran haber unido los continentes en el pasado. Fósiles de Helechos y Reptiles, que con las barreras geográficas actuales, serian imposible que pudieran atravesar los océanos y los casquetes polares. Para animales poiquilotermos (sin temperatura corporal constante), como los reptiles, estas barreras son infranqueables. Igualmente les ocurre a los Helechos, que son plantas muy endémicas, características de los lugares concretos que habitan, que requieren condiciones de humedad y temperatura muy particulares para reproducirse y expandirse.
En estas ilustraciones se representa la evolución de los continentes desde principios de la era secundaria, hace unos 200 millones de años, hasta la actualidad. La teoría de la Deriva Contimental sirvió de avansadilla para mostrar una Tierra mucho mas dinámica de lo que la ciencia contemplaba en esos tiempos. (Ilustración tomada del libro "Continentes en colisión" de la colección "Planeta Tierra"de Time-Life.)
- Existencia de series de rocas y acontecimientos geológicos pasados iguales, a ambos lados del atlántico.
- Cordilleras que se interrumpen a un lado del océano atlántico, para continuar por el otro lado, manteniendo su alineación.
- Glaciares en África, Arrecifes de Coral en continentes muy al norte de las zonas tropicales donde tienen restringido su hábitat actual.
- Yacimientos de Carbón, procedentes de bosques templados y húmedos, en áreas continentales actuales muy frías.
Todos estos eventos, hacían pensar en una variación climática extrema en el pasado, que pudiera haber llevado a una variación considerable del eje de rotación terrestre; o a la intrépida idea de que los continentes se pudieran mover y llevar grabado en sus rocas el clima de las zonas por donde han pasado en otras épocas.
- La distribución de los mamíferos en la actualidad y de otras especies, se hacía imposible de comprender, sin admitir una proximidad continental en el pasado.
Las ideas osadas y atrevidas de Wegener, admitían que los continentes habían estado unidos en el pasado, formando un gran continente que denominó Pangea. Dicho continente se había fragmentado en dos grande de masas continentales primero: Laurasia al norte y Gondwana al sur, para después dividirse en los actuales continentes, a medida que se movían hasta alcanzar su posición actual.
Dichas ideas chocaron frontalmente con las teorías dominantes del momento, que proponían un enfriamiento y contracción subsiguiente de la corteza terrestre, para explicar la formación de las montañas; y de puentes intercontinentales o islas oceánicas, que posteriormente se habían hundido, para explicar la distribución de la vida actual y pasada en la Tierra.
Wegener era un romántico y un visionario que perdió su vida en su amada Groenlandia, intentando demostrar su visión de la Tierra. Pero su esfuerzo no quedaría en vano y sus ideas cuajaron en un grupo de científicos que veían que existían muchas pruebas de que los continentes no siempre habían estado en la posición que ahora ocupaban, y que las teorías de la contracción térmica y los puentes intercontinentales, eran incompatibles con la existencia de los dos tipos de corteza terrestre: la de los continentes y la de los océanos, que por esa época se empezaban a descubrir.
Pero seguía siendo un misterio las fuerzas que movían a los continentes. Las que proponía Wegener, eran matemáticamente imposibles de que pudieran arrastrar a los continentes sobre el fondo rocoso de los océanos, sin que antes, esas mismas fuerzas, frenaran la rotación de la propia Tierra.
A pesar de las muchas pruebas, las ideas de Wegener quedaron relegadas por las oficiales y la segunda guerra mundial. Pero esa misma guerra supondría un revulsivo a modelo oficial de la Tierra, al desarrollarse con fines bélicos, instrumentos de observación del fondo oceánico.
A la vanguardia de la investigación oceánica en la década de 1940, se encontraba el joven físico norteamericano Maurice Ewing, quien junto a sus compatriotas.
En física, la energía interna (U) de un sistema intenta ser un reflejo de la energía a escala macroscópica. Más concretamente, es la suma de:
- la energía cinética interna, es decir, de las sumas de las energías cinéticas de las individualidades que lo forman respecto al centro de masas del sistema,
- la energía potencial interna, que es la energía potencial asociada a las interacciones entre estas individualidades.1
La energía interna no incluye la energía cinética traslacional o rotacional del sistema como un todo. Tampoco incluye la energía potencial que el cuerpo pueda tener por su localización en un campo gravitacional o electrostático externo.
Todo cuerpo posee una energía acumulada en su interior equivalente a la energía cinética interna más la energía potencial interna.
- En un gas ideal monoatómico bastará con considerar la energía cinética de traslación de sus átomos.
- En un gas ideal poliatómico, deberemos considerar además la energía vibracional y rotacional de las mismas.
- En un líquido o sólido deberemos añadir la energía potencial que representa las interacciones moleculares.
Desde el punto de vista de la termodinámica, en un sistema cerrado (o sea, de paredes impermeables), la variación total de energía interna es igual a la suma de las cantidades de energía comunicadas al sistema en forma de calor y de trabajo 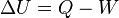 (En termodinámica se considera el trabajo negativo cuando este entra en el sistema termodinámico, positivo cuando sale). Aunque el calor transmitido depende del proceso en cuestión, la variación de energía interna es independiente del proceso, sólo depende del estado inicial y final, por lo que se dice que es una función de estado. Del mismo modo (En termodinámica se considera el trabajo negativo cuando este entra en el sistema termodinámico, positivo cuando sale). Aunque el calor transmitido depende del proceso en cuestión, la variación de energía interna es independiente del proceso, sólo depende del estado inicial y final, por lo que se dice que es una función de estado. Del mismo modo  es una diferencial exacta, a diferencia de es una diferencial exacta, a diferencia de  , que depende del proceso. , que depende del proceso.
MAQUINAS TERMICAS
Máquina térmica

Rotores de un compresor de doble tornillo, un tipo de compresor volumétrico rotativo.

Compresor rotodinámico axial.
Por el contrario, en una máquina hidráulica, que es otro tipo de máquina de fluido, la variación de densidad es suficientemente pequeña como para poder desacoplar el análisis de los efectos mecánicos y el análisis de los efectos térmicos, llegando a despreciar los efectos térmicos en gran parte de los casos. Tal es el caso de una bomba hidráulica, a través de la cual pasa líquido. Alejándose de lo que indica la etimología de la palabra «hidráulica», también puede considerarse como máquina hidráulica un ventilador, pues, aunque el aire es un fluido compresible, la variación de volumen específico no es muy significativa con el propósito de que no se desprenda la capa límite.
En una máquina térmica, la compresibilidad del fluido no es despreciable y es necesario considerar su influencia en la transformación de energía.
Máquina térmica y motor térmico[editar]
En un principio se podría definir a una máquina térmica como un dispositivo, equipo o una instalación destinada a la producción de trabajo en virtud de un aporte calórico. Aunque en algunas definiciones se identifican como sinónimos los términos «máquina térmica motora» y « motor térmico», en otras se diferencian ambos conceptos. Al diferenciarlos, se considera que un motor térmico es un conjunto de elementos mecánicos que permite obtener energía mecánica a partir de la energía térmica obtenida mediante una reacción de combustión o una reacción nuclear. Un motor térmico dispone de lo necesario para obtener energía térmica, mientras que una máquina térmica motora necesita energía térmica para funcionar, mediante un fluido que dispone de más energía a la entrada que a la salida.
Clasificación[editar]
Según el sentido de transferencia de energía[editar]
Las máquinas térmicas pueden clasificarse, según el sentido de transferencia de energía, en:
- Máquinas térmicas motoras, en las cuales la energía del fluido disminuye al atravesar la máquina, obteniéndose energía mecánicaen el eje.
- Máquinas térmicas generadoras, en las cuales la energía del fluido aumenta al atravesar la máquina, precisándose energía mecánica en el eje.
Según el principio de funcionamiento[editar]
Atendiendo al principio de funcionamiento, las máquinas térmicas se clasifican en:
- Máquinas volumétricas o máquinas de desplazamiento positivo, cuyo funcionamiento está basado en principios mecánicos e hidrostáticos, de manera que el fluido en algún instante está contenido en un volumen limitado por los elementos de la máquina. En este tipo de máquinas el flujo es pulsatorio. Se dividen a su vez en dos tipos según el movimiento del órgano propulsor: alternativas, cuyo movimiento es rectilíneo; y rotativas, cuyo movimiento es circular.
- Turbomáquinas, cuyo funcionamiento está basado en el intercambio de cantidad de movimiento entre el fluido y un rodete. En estas máquinas el flujo es continuo.
Teniendo en cuenta lo anterior, podemos clasificar las máquinas térmicas tal como se recoge en el cuadro siguiente.
Balance de energía en una máquina térmica[editar]
donde;
- Q es el calor entregado al sistema. Será negativo cuando el calor sea entregado por el sistema.
- W es el trabajo entregado al sistema, en forma de trabajo mecánico y energía de presión. Será negativo cuando el calor sea entregado por el sistema.
- El subíndice in representa la materia que entra al sistema.
- El subíndice out representa la materia que sale del sistema.
- h es la entalpía por unidad de masa del flujo
- V2/2 es la energía cinética por unidad de masa del flujo.
- gz es la energía potencial por unidad de masa del flujo
Haciendo la derivada de la expresión anterior respecto al tiempo, se obtiene:
Debe tenerse en cuenta que en máquinas generadoras, puede aparecer esta expresión con el signo de Wcambiado, para que se exprese el trabajo entregado por la máquina y así W sea positivo.
Simplificaciones[editar]
La ecuación que expresa el balance de energía puede simplificarse en los siguientes casos:
- Sistema en reposo
Cuando el sistema está en reposo, tal como en máquinas estacionarias, las variaciones de energía potencial y energía cinética serán nulas.
 - Régimen permanente
Cuando la máquina funciona en régimen permanente, las cantidades de masa y energía que entran son iguales a las que salen, pues de lo contrario variarían esa cantidades dentro del sistema.   - Variación de energía potencial despreciable
En la mayoría de las máquinas térmicas, diferencia de energía potencial del flujo que sale respecto al que entra es poco significativo en comparación con los otros términos asociados a la energía del flujo.
 - Sistemas adiabáticos

- La superficie externa del sistema está bien aislada térmicamente.
- La superficie externa del sistema es muy pequeña.
- La diferencia de temperaturas entre el flujo y el entorno del sistema es pequeña.
- El fluido pasa a través de la máquina tan rápido que apenas hay tiempo para que sea significativa la transferencia de calor por unidad de masa.
Máquina térmica en régimen permanente con variación de energía potencial despreciable[editar]
En una máquina térmica que funciona en régimen permanente en la cual se desprecie la variación de energía potencial, la expresión el primer principio de la termodinámica puede expresarse como
En los ciclos termodinámicos asociados a la turbina de vapor, la energía cinética específica puede considerarse despreciable frente a la entalpía, resultando
Rendimiento[editar]

Diagrama h- S de vapor de agua, en el que se muestran en rojo dos expansiones entre dos isobarasdistintas. La presión de salida es una condición de contorno para el proceso. Con una expansión isoentrópica entre las presiones de entrada y de salida se obtendría mayor salto entálpico.
Para el cálculo del rendimiento, se relaciona la energía obtenida, ya sea en forma de incremento de energía en el fluido o de energía mecánica suministrada por la máquina, entre la máxima energía que se podría obtener en las condiciones de contorno.
Rendimiento de una máquina térmica motora[editar]
- Rendimiento interno
El trabajo específico máximo que puede obtenerse en la expansión de un fluido está definido por la diferencia de entalpías entre el fluido a la entrada y las condiciones isoentrópicas a la presión de salida. En cambio el trabajo real es menor a éste debido al aumento de la entropía. 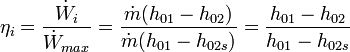
- Rendimiento mecánico
El rendimiento mecánico es la relación entre potencia efectiva ((  ), que es la potencia obtenida en el eje, y la potencia interna ((  ), que es la variación por unidad de tiempo de la energía del fluido. La potencia efectiva resulta de restar a la potencia indicada menos la potencia de pérdidas mecánicas (  ), que es disipada el rozamiento de elementos mecánicos ( cojinetes, retenes, etc.) y en el accionamiento de elementos auxiliares ( bomba de aceite, ventiladores, etc.) 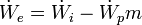 
- Rendimiento isoentrópico
El rendimiento isoentrópico relaciona la potencia obtenida en el eje con potencia máxima del proceso isoentrópico en las mismas condiciones de contorno.

Rendimiento de una máquina térmica generadora[editar]
- Rendimiento interno
El trabajo específico mínimo para comprimir un fluido desde un estado térmico hasta una presión determinada es igual al salto entálpico del correspondiente proceso isoentrópico, de forma que un proceso real presentará mayor diferencia de entalpías del fluido entre la entrada y la salida. 
- Rendimiento mecánico
El rendimiento mecánico es la relación entre potencia efectiva ((  ), que es la potencia obtenida en el eje, y la potencia interna ((  ), que es la variación por unidad de tiempo de la energía del fluido. La potencia efectiva resulta de restar a la potencia indicada menos la potencia de pérdidas mecánicas (  ), que es disipada el rozamiento de elementos mecánicos ( cojinetes, retenes, etc.) y en el accionamiento de elementos auxiliares ( bomba de aceite, ventiladores, etc.) 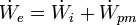 
- Rendimiento isoentrópico
El rendimiento isoentrópico relaciona potencia mínima del proceso isoentrópico en las mismas condiciones de contorno con la potencia suministrada en el eje.

GASES
Se denomina gas (palabra inventada por el científico flamenco Jan Baptista van Helmont en el siglo XVII, sobre el latínchaos1 ) al estado de agregación de la materia en el cual, bajo ciertas condiciones de temperatura y presión, sus moléculas interaccionan solo débilmente entre sí, sin formar enlaces moleculares, adoptando la forma y el volumen del recipiente que las contiene y tendiendo a separarse, esto es, expandirse, todo lo posible por su alta energía cinética. Los gases son fluidosaltamente compresibles, que experimentan grandes cambios de densidad con la presión y la temperatura. Las moléculas que constituyen un gas casi no son atraídas unas por otras, por lo que se mueven en el vacío a gran velocidad y muy separadas unas de otras, explicando así las propiedades:
-
- Las moléculas de un gas se encuentran prácticamente libres, de modo que son capaces de distribuirse por todo el espacio en el cual son contenidos. Las fuerzas gravitatorias y de atracción entre las moléculas son despreciables, en comparación con la velocidad a que se mueven sus moléculas.
- Los gases ocupan completamente el volumen del recipiente que los contiene.
- Los gases no tienen forma definida, adoptando la de los recipientes que las contiene.
- Pueden comprimirse fácilmente, debido a que existen enormes espacios vacíos entre unas moléculas y otras.
A temperatura y presión ambientales los gases pueden ser elementos como el hidrógeno, el oxígeno, el nitrógeno, el cloro, el flúor y los gases nobles, compuestos como el dióxido de carbono o el propano, o mezclas como el aire.
Los vapores y el plasma comparten propiedades con los gases y pueden formar mezclas homogéneas, por ejemplo vapor de agua y aire, en conjunto son conocidos como cuerpos gaseosos, estado gaseoso o fase gaseosa. -
LEY DE LOS GASES
Existen diversas leyes derivadas de modelos simplificados de la realidad que relacionan la presión, el volumen y la temperatura de un gas.
Ley de Boyle-Mariotte
La Ley de Boyle-Mariotte (o Ley de Boyle), formulada por Robert Boyle y Edme Mariotte, es una de las leyes de los gases que relaciona el volumen y la presión de una cierta cantidad de gas mantenida a temperatura constante. La ley dice que a una temperatura constante y para una masa dada de un gas el volumen del gas varia de manera inversamente proporcional a la presión absoluta del recipiente:
Ley de Charles
A una presión dada, el volumen ocupado por una cierta cantidad de un gas es directamente proporcional a su temperatura.
Matemáticamente la expresión sería:
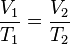 o o  . .
en términos generales:
(V1 * T2) = (V2 * T1)
Ley de Gay-Lussac
La presión de una cierta cantidad de gas, que se mantiene a volumen constante, es directamente proporcional a la temperatura:

Es por esto que para poder envasar gas, como gas licuado, primero ha de enfriarse el volumen de gas deseado, hasta una temperatura característica de cada gas, a fin de poder someterlo a la presión requerida para licuarlo sin que se sobrecaliente y eventualmente, explote. 
Ley general de los gases
Combinando las tres leyes anteriores se obtiene:

Ley de los gases ideales
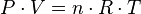
El valor de R depende de las unidades que se estén utilizando:
- R = 0,082 atm·l·K−1·mol−1 si se trabaja con atmósferas y litros
- R = 8,31451 J·K−1·mol−1 si se trabaja en Sistema Internacional de Unidades
- R = 1,987 cal·K−1·mol−1
- R = 8,31451 10−10 erg ·K−1·mol−1
- R = 8,317x10−3 (m³)(Kpa)/(mol)(K) si se trabaja con metros cúbicos y kilo pascales
De esta ley se deduce que un mol (6,022 x 10^23 átomos o moléculas) de gas ideal ocupa siempre un volumen igual a 22,4 litros a 0 °C y 1 atmósfera. Véase también Volumen molar. También se le llama la ecuación de estado de los gases, ya que solo depende del estado actual en que se encuentre el gas.
GASES REALES
Si se quiere afinar más, o si se quiere medir el comportamiento de algún gas que escapa al comportamiento ideal, habrá que recurrir a las ecuaciones de los gases reales, que son variadas y más complicadas cuanto más precisas. 
Los gases reales no se expanden infinitamente, sino que llegaría un momento en el que no ocuparían más volumen. Esto se debe a que entre sus partículas, ya sean átomoscomo en los gases nobles o moléculas como en el (O 2) y la mayoría de los gases, se establecen unas fuerzas bastante pequeñas, debido a los cambios aleatorios de sus cargas electrostáticas, a las que se llama fuerzas de Van der Waals.
El comportamiento de un gas suele concordar más con el comportamiento ideal cuanto más sencilla sea su fórmula química y cuanto menor sea su reactividad ( tendencia a formar enlaces). Así, por ejemplo, los gases nobles al ser moléculas monoatómicas y tener muy baja reactividad, sobre todo el helio, tendrán un comportamiento bastante cercano al ideal. Les seguirán los gases diatómicos, en particular el más liviano hidrógeno. Menos ideales serán los triatómicos, como el dióxido de carbono; el caso del vapor de agua aún es peor, ya que la molécula al ser polar tiende a establecer puentes de hidrógeno, lo que aún reduce más la idealidad. Dentro de los gases orgánicos, el que tendrá un comportamiento más ideal será el metano, perdiendo idealidad a medida que se engrosa la cadena de carbono. Así, el butano es de esperar que tenga un comportamiento ya bastante alejado de la idealidad. Esto es, porque cuanto más grande es la partícula constituyente del gas, mayor es la probabilidad de colisión e interacción entre ellas, factor que hace disminuir la idealidad. Algunos de estos gases se pueden aproximar bastante bien mediante las ecuaciones ideales, mientras que en otros casos hará falta recurrir a ecuaciones reales muchas veces deducidas empíricamente a partir del ajuste de parámetros.
También se pierde la idealidad en condiciones extremas, como altas presiones o bajas temperaturas. Por otra parte, la concordancia con la idealidad puede aumentar si trabajamos a bajas presiones o altas temperaturas. También por su estabilidad química.
COMPORTAMIENTO DE LOS GASES
Cualquier gas se considera como un fluido, porque tiene las propiedades que le permiten comportarse como tal.
Sus moléculas, en continuo movimiento, colisionan elásticamente entre sí y contra las paredes del recipiente que contiene al gas, contra las que ejercen una presión permanente. Si el gas se calienta, esta energía calorífica se invierte en energía cinética de las moléculas, es decir, las moléculas se mueven con mayor velocidad, por lo que el número de choques contra las paredes del recipiente aumenta en número y energía. Como consecuencia la presión del gas aumenta, y si las paredes del recipiente no son rígidas, el volumen del gas aumenta.
Un gas tiende a ser activo químicamente debido a que su superficie molecular es también grande, es decir, al estar sus partículas en continuo movimiento chocando unas con otras, esto hace más fácil el contacto entre una sustancia y otra, aumentando la velocidad de reacción en comparación con los líquidos o los sólidos.
Para entender mejor el comportamiento de un gas, siempre se realizan estudios con respecto al gas ideal, aunque éste en realidad nunca existe y las propiedades de éste son:
- Una sustancia gaseosa pura está constituida por moléculas de igual tamaño y masa. Una mezcla de sustancias gaseosas está formada por moléculas diferentes en tamaño y masa.
- Debido a la gran distancia entre unas moléculas y otras y a que se mueven a gran velocidad, las fuerzas de atracción entre las moléculas se consideran despreciables.
- El tamaño de las moléculas del gas es muy pequeño, por lo que el volumen que ocupan las moléculas es despreciable en comparación con el volumen total del recipiente. La densidad de un gas es muy baja.
- Las moléculas de un gas se encuentran en constante movimiento a gran velocidad, por lo que chocan elásticamente de forma continua entre sí y contra las paredes del recipiente que las contiene.
Para explicar el comportamiento de los gases, las nuevas teorías utilizan tanto la estadística como la teoría cuántica, además de experimentar con gases de diferentes propiedades o propiedades límite, como el UF6, que es el gas más pesado conocido.
Un gas no tiene forma ni volumen fijo; se caracteriza por la casi nula cohesión y la gran energía cinética de sus moléculas, las cuales se mueven.
Cambios de densidad
El efecto de la temperatura y la presión en los sólidos y líquidos es muy pequeño, por lo que típicamente la compresibilidad de un líquido o sólido es de 10 −6 bar−1(1 bar=0,1 MPa) y el coeficiente de dilatación térmica es de 10 −5 K−1.
Por otro lado, la densidad de los gases es fuertemente afectada por la presión y la temperatura. La ley de los gases ideales describe matemáticamente la relación entre estas tres magnitudes:
Eso significa que un gas ideal a 300 K (27 °C) y 1 atm duplicará su densidad si se aumenta la presión a 2 atm manteniendo la temperatura constante o, alternativamente, se reduce su temperatura a 150 K manteniendo la presión constante.
Presión de un gas
En el marco de la teoría cinética, la presión de un gas es explicada como el resultado macroscópico de las fuerzas implicadas por las colisiones de las moléculas del gas con las paredes del contenedor. La presión puede definirse por lo tanto haciendo referencia a las propiedades microscópicas del gas.
En efecto, para un gas ideal con N moléculas, cada una de masa m y moviéndose con una velocidad aleatoria promedio vrms contenido en un volumen cúbico V, las partículas del gas impactan con las paredes del recipiente de una manera que puede calcularse de manera estadística intercambiando momento lineal con las paredes en cada choque y efectuando una fuerza neta por unidad de área, que es la presión ejercida por el gas sobre la superficie sólida.
La presión puede calcularse como:
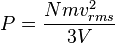 (gas ideal)
Este resultado es interesante y significativo no solo por ofrecer una forma de calcular la presión de un gas sino porque relaciona una variable macroscópica observable, la presión, con la energía cinética promedio por molécula, 1/2 mvrms², que es una magnitud microscópica no observable directamente. Nótese que el producto de la presión por el volumen del recipiente es dos tercios de la energía cinética total de las moléculas de gas contenidas.
PROCESO ISOTÉRMICO
Se denomina proceso isotérmico o proceso isotermo al cambio reversible en un sistema Termodinámica, siendo dicho cambio a temperatura constante en todo el sistema. La comprensión o expansión de un gas ideal puede llevarse acabo colocando el gas en contacto térmico con otro sistema de capacidad calorífica muy grande y a la misma temperatura que el gas.
Este otro sistema se conoce como foco calorífico. De esta manera el calor, se transfiere muy lentamente, permitiendo que el gas se expanda realizando trabajo.Como la energía interna de un gas ideal solo depende de la temperatura
-
PROCESO ISOTÉRMICO DE UN
GAS
Una expansión isotérmica es un proceso en el cual un gas se expande (o contrae), manteniendo la temperatura constante durante dicho proceso, es decir que T 1 = T 2 para los estados inicial (1) y final (2) del proceso isotérmico. Aplicando el primer principio de la termodinámica se obtiene: 
Entonces integrando la expresión anterior, tomando como estado inicial el estado 1 y estado final el estado 2, se obtiene:
 ..........(1) ..........(1)

Pero la fuerza  se puede expresar en función de la presión que se ejerce el gas, y el desplazamiento 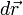 se puede escribir como dx, entonces: 
Pero Adx equivale a dV, el aumento en el volumen del gas durante esta pequeña expansión, entonces el trabajo efectuado por el gas sobre los alrededores como resultado de la expansión es:
 ..........(2) ..........(2)
Ahora reemplazando (1) en (2) se puede integrar:
 ..........(3) ..........(3)
Pero para integrar la tercera integral, es necesario conocer la forma de variación de la presión P con el volumen, durante el proceso tratado.
En el caso de tratar con gases ideales, se tendría la relación:
 ..........(4) ..........(4)
Por lo tanto reemplazando (4) en (3) se tiene que:
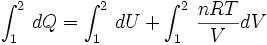
Como los valores n y R son constantes para cada gas ideal, y en este caso la temperatura también es constante, éstas pueden salir fuera de la integral obteniéndose:
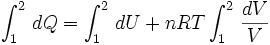
Ahora integrando:
![[Q]_1^2 = [U]_1^2 + nRT[\ln V]_1^2](https://upload.wikimedia.org/math/9/b/b/9bb7def5b45c1c793290a37d2aafc98d.png) 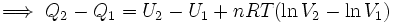  ..........(5) ..........(5)
Pero se sabe que la energía interna depende sólo de la temperatura ( Ver: La energía interna como función de la temperatura), y como en este proceso ésta se mantiene constante, no hay cambio en la energía interna del gas, por lo que la expresión (5) se reduce a: 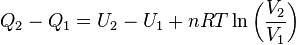  
Por lo tanto, en una expansión isotérmica de un gas perfecto, el calor de entrada es igual al trabajo efectuado por el gas.
Un proceso isobárico es un proceso termodinámico que ocurre a presión constante. La Primera Ley de la Termodinámica, para este caso, queda expresada como sigue:
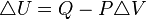 ,
Donde:
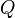 = Calor transferido. = Calor transferido.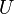 = Energía interna. = Energía interna.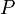 = Presión. = Presión. = Volumen. = Volumen.
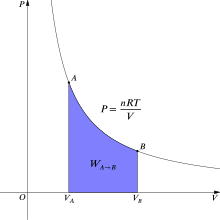
En un diagrama P-V, un proceso isobárico aparece como una línea horizontal.
Gráfica Volumen vs Presión: en el proceso isobárico la presión es constante. El trabajo (W) es la integral de la presión respecto al volumen.
Una expansión isobárica es un proceso en el cual un gas se expande (o contrae) mientras que la presión del mismo no varía, es decir si en un estado 1 del proceso la presión es P1 y en el estado 2 del mismo proceso la presión es P2, entonces P1 = P2. La primera ley de la termodinámica nos indica que:

Integrando la expresión anterior, tomando como estado inicial el estado 1 y estado final el estado 2, se obtiene:
 ..........(1) ..........(1)

Pero la fuerza  se puede expresar en función de la presión que se ejerce el gas, y el desplazamiento 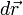 se puede escribir como dx, entonces: 
Pero Adx equivale a dV, el aumento en el volumen del gas durante esta pequeña expansión, entonces el trabajo efectuado por el gas sobre los alrededores como resultado de la expansión es:
 ..........(2) ..........(2)
Ahora reemplazando (1) en (2) se puede integrar:

Como la presión P es constante, puede salir fuera de la integral:

Integrando:
![[Q]_1^2 = [U]_1^2 + P[V]_1^2](https://upload.wikimedia.org/math/1/9/c/19cdd44053e4376e08a03df37aa01416.png)
Evaluando en los límites:
 
PROBLEMAS RESUELTOS
1.- Una cantidad de gas ocupa un volumen de 80 cm3 a una presión de 750 mm Hg. ¿Qué volumen ocupará a una presión de 1,2 atm.si la temperatura no cambia?
Como la temperatura y la masa permanecen constantes en el proceso, podemos aplicar la ley de Boyle: P1.V1 = P2.V2
Tenemos que decidir qué unidad de presión vamos a utilizar. Por ejemplo atmósferas.
Como 1 atm = 760 mm Hg, sustituyendo en la ecuación de Boyle:
-
2.- El volumen inicial de una cierta cantidad de gas es de 200 cm3 a la temperatura de 20ºC. Calcula el volumen a 90ºC si la presión permanece constante.
Como la presión y la masa permanecen constantes en el proceso, podemos aplicar la ley de Charles y Gay-Lussac:
-
El volumen lo podemos expresar en cm3 y, el que calculemos, vendrá expresado igualmente en cm3, pero la temperatura tiene que expresarse en Kelvin.
-
3.- Una cierta cantidad de gas se encuentra a la presión de 790 mm Hg cuando la temperatura es de 25ºC. Calcula la presión que alcanzará si la temperatura sube hasta los 200ºC.
Como el volumen y la masa permanecen constantes en el proceso, podemos aplicar la ley de Gay-Lussac:
-
La presión la podemos expresar en mm Hg y, la que calculemos, vendrá expresada igualmente en mm Hg, pero la temperatura tiene que expresarse en Kelvin.
-
4.- Disponemos de un recipiente de volumen variable. Inicialmente presenta un volumen de 500 cm3 y contiene 34 g de amoníaco. Si manteniendo constante la P y la T, se introducen 68 g de amoníaco, ¿qué volumen presentará finalmente el recipiente?
Ar (N)=14. Ar (H)=1.
Manteniendo constante la P y la T, el volumen es directamente proporcional al número de moles del gas. El mol de amoníaco, NH3, son 17 g luego:
Inicialmente hay en el recipiente 34 g de gas que serán 2 moles y al final hay 102 g de amoníaco que serán 6 moles.
-
5.- Un gas ocupa un volumen de 2 l en condiciones normales. ¿Qué volumen ocupará esa misma masa de gas a 2 atm y 50ºC?
Como partimos de un estado inicial de presión, volumen y temperatura, para llegar a un estado final en el que queremos conocer el volumen, podemos utilizar la ley combinada de los gases ideales, pues la masa permanece constante:
-
-
PROCESO ISOCÓRICO
Un proceso isocórico, también llamado proceso isométrico o isovolumétrico es un proceso termodinámico en el cual el volumen permanece constante; 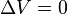 . Esto implica que el proceso no realiza trabajo presión-volumen, ya que éste se define como: 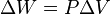 , ,
donde P es la presión (el trabajo es positivo, ya que es ejercido por el sistema).
En un diagrama P-V, un proceso isocórico aparece como una línea vertical.

Proceso isocórico en un diagrama P-V.
CÁLCULO DEL TRABAJO
Cálculo del Trabajo (W)
Puesto que no existe desplazamiento, el trabajo realizado por el gas es nulo.

Cálculo de la Variación de la Energía Interna (ΔU)
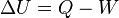  
para un proceso isocórico, es decir a volumen constante, todo el calor que transfiramos al sistema aumentará a su energía interna U.
Cálculo del calor entregado
Si la cantidad de gas permanece constante, entonces el incremento de energía será proporcional al incremento de temperatura, 
PROCESO ADIABÁTICO
-
El término adiabático hace referencia a volúmenes que impiden la transferencia de calor con el entorno. Una pared aislada se aproxima bastante a un límite adiabático. Otro ejemplo es la temperatura adiabática de llama, que es la temperatura que podría alcanzar una llama si no hubiera pérdida de calor hacia el entorno. En climatización los procesos de humectación (aporte de vapor de agua) son adiabáticos, puesto que no hay transferencia de calor, a pesar que se consiga variar la temperatura del aire y su humedad relativa.
El calentamiento y enfriamiento adiabático son procesos que comúnmente ocurren debido al cambio en la presión de un gas. Esto puede ser cuantificado usando la ley de los gases ideales.
En otras palabras se considera proceso adiabático a un sistema especial en el cual no se pierde ni tampoco se gana energía calorífica. Esto viene definido según la primera ley de termodinámica describiendo que Q=0
Si se relaciona el tema del proceso adiabático con las ondas, se debe tener en cuenta que el proceso o carácter adiabático solo se produce en las ondas longitudinales
-
Durante un proceso adiabático, la energía interna del fluido que realiza el trabajo debe necesariamente decrecer.
FORMULACIÓN MATEMÁTICA
La ecuación matemática que describe un proceso adiabático en un gas (si el proceso es reversible) es 
donde P es la presión del gas, V su volumen y 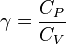
Derivación de la expresión[editar]
La definición de un proceso adiabático es que la transferencia de calor del sistema es cero,  . 
donde U es la energía interna del sistema y W es el trabajo realizado por el sistema. Cualquier trabajo (W) realizado debe ser realizado a expensas de la energía U, mientras que no haya sido suministrado calor Q desde el exterior. El trabajo W realizado por el sistema se define como 
Sin embargo, P no permanece constante durante el proceso adiabático sino que por el contrario cambia junto con V.
en la fórmula:

hacemos un pequeño cambio entonces quedaría así:
 ......(1)
Ahora derivando la fórmula de del trabajo e integrándola a la vez tenemos :
 =  .....(2)
Ahora reemplazamos la (2) en la (1) :
Ahora sabemos que "K" es una constante , por lo cual esta sale de la integral:
luego vemos que nos queda todo en función del volumen entonces lo integramos:
como sabemos que :
entonces reemplazamos en la ecuación:
y multiplicamos :
luego de resolver la ecuación nos quedará esta forma:
y por definición nos quedaría :

que al final nos dará:
y esto será igual al trabajo :
también podemos tener una variante :
Deseamos conocer cómo los valores de  y  se relacionan entre sí durante el proceso adiabático. Para ello asumiremos que el sistema es un gas monoatómico, por lo que 

Ahora sustituyendo las ecuaciones (2) y (3) en la ecuación (1) obtenemos

simplificando

dividiendo ambos lados de la igualdad entre PV

Aplicando las normas del cálculo diferencial obtenemos que

que se puede expresar como

Para ciertas constantes 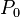 y  del estado inicial. Entonces 

elevando al exponente ambos lados de la igualdad

eliminando el signo menos

por lo tanto

y

- PROCESO DIATÉRMICO
Se refieren a que el sistema tiene un intercambio de energía con los alrededores, un ejemplo, nosotros, los seres humanos, somos sistemas diatérmicos, ya que estamos intercambiando energía con nuestro ambiente.
La manera usual de definirlo es que un límite es diatérmico cuando permite el flujo de calor a través de él.
Un ejemplo, nosotros, los seres humanos, somos sistemas diatérmicos, ya que estamos intercambiando energía con nuestro ambiente. Diatérmico también puede entenderse por isotérmico , significa que no hay cambio de temperatura debido a una pared diatérmica que aísla el sistema del medio ambiente, tener bien en cuenta las definiciones de sistema , medio ambiente y universo. La manera usual de definirlo es que un límite es diatérmico cuando permite el flujo de calor a través de él. De nuevo, preferimos evitar esta segunda definición debido a la dificultad de definir calor.
-
Otra definición:
En proceso diatérmico es aquél en el que se intercambia calor sin intercambiar masa.
EJEMPLOS:
El enfriamiento del té o el café en la taza es un proceso diatérmico.
- El calentamiento de los alimentos cuando los cocinamos.
- El frío que hace en casa en invierno Por estar frío fuera
El calor que hace con la calefacción prendida por estar caliente el agua que circula por el radiador.
La refrigeración de un chip a través del disipador de calor
- La fusión de los cubitos de hielo a temperatura ambiente
- El calentamiento de alimentos en una cazuela
El enfriamiento de los alimentos
- La subida de temperatura de un termómetro
- El enfriamiento de una bañera.
PROBLEMAS RESUELTOS
Un recipiente hermético que mantiene
su volumen constante contiene gas
. Si se le suministran 50 calorías
desde el exterior ¿que variación de
energía interna presenta?
1. Esquema
2. Datos 3. Incógnita
Q= 50 cal AEi=? J
No hay incremento de volumen
AV=0
4. Ecuación
AE= Q-Tr
• Al no aver variación de volumen no
se efectúa trabajo, por lo que este es
cero, Tr=0.
• Por tanto la ecuación anterior se
reduce a AE i=Q
El calor es positivo debido a que entra al sistema.
5. Conversiones 6. Sust. y Op. 7. Resultado
1cal= 4.2J AEi= Q= 210J AEi= 210J
Q= 50cal (4.2J/1cal) =210 J
La variación de energía interna aumenta debido a que se le suministro calor al sistema.
*- Un recipiente cerrado de 2 l. contiene oxígeno a 200ºC y 2 atm. Calcula:
a) Los gramos de oxígeno contenidos en el recipiente.
b) Las moléculas de oxígeno presentes en el recipiente.
Ar(O)=16.
a) Aplicando la ecuación general de los gases PV=nRT podemos calcular los moles de oxígeno:
* Tenemos 4,88 g de un gas cuya naturaleza es SO2 o SO3. Para resolver la duda, los introducimos en un recipiente de 1 l y observamos que la presión que ejercen a 27ºC es de 1,5 atm. ¿De qué gas se trata?
Ar(S)=32.Ar(O)=16.
Aplicando la ecuación general de los gases PV=nRT podemos calcular los moles correspondientes a esos 4,88 gramos de gas:
ONDAS
En física, una onda (del latín unda) consiste en la propagación de una perturbación de alguna propiedad del espacio, por ejemplo, densidad, presión, campo eléctrico o campo magnético, implicando un transporte de energía sin transporte de materia. El espacio perturbado puede contener materia (aire, agua, etc) o no (vacío).
La magnitud física cuya perturbación se propaga en el medio se expresa como una función tanto de la posición como del tiempo  . Matemáticamente se dice que dicha función es una onda si verifica la ecuación de ondas: 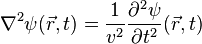
donde  es la velocidad de propagación de la perturbación. Por ejemplo, ciertas perturbaciones de la presión de un medio, llamadas sonido, verifican la ecuación anterior, aunque algunas ecuaciones no lineales también tienen soluciones ondulatorias, por ejemplo, un solitón.
Ondas superficiales en agua.
Una vibración puede definir las características necesarias y suficientes que caracterizan un fenómeno como onda. El término suele ser entendido intuitivamente como el transporte de perturbaciones en el espacio, donde se considera el espacio como un medio en el que pueden producirse y propagarse dichas perturbaciones a través de él, al variar alguna de sus propiedades medibles.
La teoría de ondas se conforma como una característica rama de la física que se ocupa de las propiedades de los fenómenos ondulatorios independientemente de cual sea su origen físico (Ostrovsky y Potapov, 1999). Una peculiaridad de estos fenómenos ondulatorios es que a pesar de que el estudio de sus características no depende del tipo de onda en cuestión, los distintos orígenes físicos que provocan su aparición les confieren propiedades muy particulares que las distinguen de unos fenómenos a otros. Por ejemplo, la acústica se diferencia de la óptica en que las ondas sonoras están relacionadas con aspectos más mecánicos que las ondas electromagnéticas (que son las que gobiernan los fenómenos ópticos). Conceptos tales como masa, cantidad de movimiento, inercia o elasticidad son conceptos importantes para describir procesos de ondas sonoras, a diferencia de en las ópticas, donde estas no tienen una especial relevancia. Por lo tanto, las diferencias en el origen o naturaleza de las ondas producen ciertas propiedades que caracterizan cada onda, manifestando distintos efectos en el medio en que se propagan (por ejemplo, en el caso del aire: vórtices, ondas de choque; en el caso de los sólidos: dispersión; y en el caso del electromagnetismo presión de radiación).
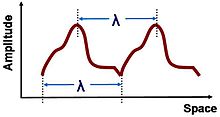
Longitud de onda λ, se puede medir entre dos puntos correspondientes en una forma de onda.
Una onda transversal es una onda en la que cierta magnitud vectorial presenta oscilaciones en alguna dirección perpendicular a la dirección de propagación. Para el caso de una onda mecánica de desplazamiento, el concepto es ligeramente sencillo, la onda es transversal cuando las vibraciones de las partículas afectadas por la onda son perpendiculares a la dirección de propagación de la onda. Las ondas electromagnéticas son casos especiales de ondas transversales donde no existe vibración de partículas, pero los campos eléctricos y magnéticos son siempre perpendiculares a la dirección de propagación, y por tanto se trata de ondas transversales.
Si una onda transversal se mueve en el plano x-positivo, sus oscilaciones van en dirección arriba y abajo que están en el plano y-z.
Manteniendo una traza comparamos la magnitud del movimiento aleatorio y el desplazamiento en instantes sucesivos y se aprecia el avance de la onda. Transcurrido un tiempo la persistencia de la traza muestra como todos los puntos pasan por todos los estados de vibración. Sin embargo para conocer como cambia el desplazamiento con el tiempo resulta más práctico observar otra gráfica que represente el movimiento de un punto. Los puntos en fase con el seleccionado vibran a la vez y están separados por una longitud de onda. La velocidad con que se propaga la fase es el cociente entre esa distancia y el tiempo que tarda en llegar. Cualquier par de puntos del medio en distinto estado de vibración están desfasados y si la diferencia de fase es 90º diremos que están en oposición. En este caso los dos puntos tienen siempre valor opuesto del desplazamiento como podemos apreciar en el registro temporal. Este tipo de onda transversal igualmente podría corresponder a las vibraciones de los campos eléctrico y magnético en las ondas electromagnéticas. Una onda electromagnética que puede propagarse en el espacio vacío no produce desplazamientos puntuales de masa.

La luz es un ejemplo de onda transversal electromagnética.
Ejemplos de onda tansversales incluyen ondas sísmicas secundarias, el movimiento de los campos eléctricos (E) y magnéticos (V) en una onda plana electromagnética, donde ambos oscilan perpendicularmente entre sí, así como en dirección de la transferencia de energía. Por lo tanto, una onda electromagnética consta de dos ondas transversales, la luz visible es un ejemplo de onda electromagnética. Véase Espectro electromagnético para información de distintos tipos de onda electromagnética.
Propagación de una onda transversal esférica en una cuadrícula de 2 dimensiones (modelo empírico).
Una onda longitudinal es una onda mecánica en la que el movimiento de oscilación de las partículas del medio es paralelo a la dirección de propagación de la onda. Las ondas longitudinales reciben también el nombre de ondas de presión u ondas de compresión. Algunos ejemplos de ondas longitudinales son el sonido y las ondas sísmicas de tipo P generadas en un terremoto.
En teoría de campos también pueden existir ondas no mecánicas de tipo longitudinal, aunque las ondas electromagnéticas son siempre ondas transversales, nunca longitudinales, debido a que el fotón es una partícula sin masa.
Representación de la propagación de una onda longitudinal en un reticulado de 2 dimensiones.
La primera figura ilustra el caso de una onda sonora. Si el centro de la figura es un foco puntual generador de la onda, los frentes de onda se desplazan alejándose del foco, transmitiendo el sonido a través del medio de propagación, por ejemplo aire. Por otro lado, cada partícula de un frente de onda cualquiera oscila en dirección de la propagación, esto es, inicialmente empujada en la acción por efecto del incremento de presión provocado por el foco, retornando a su posición anterior por efecto de la disminución de presión provocada por su desplazamiento, por esa razón las ondas sonoras son ondas longitudinales. Estas necesitan de un medio material (sólido, líquido o gas).
*
El período de un movimiento ondulatorio que se propaga por el eje de abscisas es de 3×10-3 s. La distancia entre dos puntos consecutivos cuya diferencia de fase es p/2 vale 30 cm. Calcular: a) La longitud de onda. b) La velocidad de propagación.
La diferencia de fase de dos puntos que distan una longitud de onda es 2p,
luego:
La velocidad de propagación de la onda es:
* La función de onda correspondiente a una onda armónica en una cuerda es Y(x, t) = 0,001 sen(314t+62,8x), escrita en el SI. a) ¿En qué sentido se mueve la onda? b) ¿Cuál es su velocidad? c) ¿Cuál es la longitud de onda, frecuencia y periodo? d) ¿Cuál es el desplazamiento máximo de un segmento cualquiera de la cuerda? e) ¿Cuál es la ecuación de la velocidad y aceleración de una particula de la cuerda que se encuentre en el punto x = – 3 cm?
El sentido en que se propaga una onda de función: 0,001 sen(314t±62,8x) es, debido al signo+, el sentido negativo del eje X.
El período, frecuencia, velocidad de propagación y longitud de onda se obtienen de dicha función:
De k = 2p/l =62,8
El desplazamiento máximo de un segmento cualquiera de la cuerda viene dado por la amplitud de la función Y(x, t). Es decir: A = 0,001 m.
La función de onda de una partícula de la cuerda que se encuentra en el punto x = 0,03 m es:
La ecuación de su velocidad:
y la de su aceleración:
5. Escribir una función que interprete la propagación de una onda que se mueve hacia la derecha a lo largo de una cuerda con velocidad de 10 ms-1, frecuencia de 60 hertz y amplitud 0,2 m.
La función de onda, en general, viene dada por: y(z, t) = A sen (wt – kz) siendo en este caso:
w = 2pn = 120p rad×s-1 = 377 rad×s-1
A = 0,2 m.
Sustituyendo estos valores en y(z, t) resulta:
y(z, t) = 0,2 sen (377t – 37,68z).
*La ecuación de una onda transversal que se propaga en una cuerda viene dada por y(x, t) =10 sen(2pt – px/0,10), escrita en el SI. Hallar: a) La velocidad de propagación de la onda. b) La velocidad y aceleración máxima de las partículas de la cuerda.
Considerando la ecuación general de la cuerda:
e identificando términos se obtiene:
La velocidad de propagación de la onda resulta entonces igual a:
La velocidad con que se mueve una partícula cualquiera de la cuerda es:
siendo su valor máximo cuando el coseno se haga la unidad. Es decir: 20p ms-1.
En cuanto a la aceleración es:
y su valor máximo: 40p2 ms-2
SONIDO
El sonido (del latín sonĭtus, por analogía prosódica con ruido, chirrido, rugido, etc.), en física, es cualquier fenómeno que involucre la propagación en forma de ondas elásticas (sean audibles o no), generalmente a través de un fluido (u otro medio elástico) que esté generando el movimiento vibratorio de un cuerpo.
El sonido humanamente audible consiste en ondas sonoras que se producen cuando las oscilaciones de la presión del aire, son convertidas en ondas mecánicas en el oído humano y percibidas por el cerebro. La propagación del sonido es similar en los fluidos, donde el sonido toma la forma de fluctuaciones de presión. 1 En los cuerpos sólidos la propagación del sonido involucra variaciones del estado tensional del medio.
La fonética acústica concentra su interés especialmente en los sonidos del habla: cómo se generan, cómo se perciben, y cómo se pueden describir gráfica o cuantitativamente.La propagación del sonido involucra transporte de energía sin transporte de materia, en forma de ondas mecánicas que se propagan a través de un medio elástico sólido, líquido o gaseoso. Entre los más comunes se encuentran el aire y el agua. No se propagan en el vacío, al contrario que las ondas electromagnéticas. Si las vibraciones se producen en la misma dirección en la que se propaga el sonido, se trata de una onda longitudinal y si las vibraciones son perpendiculares a la dirección de propagación es una onda transversal.
Transmisión del sonido en un fluido. Se produce una onda de presión por compresión, que hace que el resto de las partículas se compriman entre ellas.
FÍSICA DEL SONIDO
La física del sonido es estudiada por la acústica, que trata tanto de la propagación de las ondas sonoras en los diferentes tipos demedios continuos como la interacción de estas ondas sonoras con los cuerpos físicos.

Propagación del sonido
Ciertas características de los fluidos y de los sólidos influyen en la onda de sonido. Por eso el sonido se propaga en los sólidos y en los líquidos con mayor rapidez que en los gases. En general cuanto mayor sea la compresibilidad (1/ K) del medio tanto menor es la velocidad del sonido. También la densidad es un factor importante en la velocidad de propagación, en general cuanto menor sea la densidad (ρ), a igualdad de todo lo demás, mayor es la velocidad de la propagación del sonido. La velocidad del sonido se relaciona con esas magnitudes mediante:
En los gases, la temperatura influye tanto la compresibilidad como la densidad, de tal manera que un factor de suma importancia es la temperatura del medio de propagación.
La propagación del sonido está sujeta a algunos condicionantes. Así la transmisión de sonido requiere la existencia de un medio material donde la vibración de las moléculas es percibida como una onda sonora. En la propagación en medios compresibles como el aire, la propagación implica que en algunas zonas las moléculas de aire, al vibrar se juntan (zonas de compresión) y en otras zonas se alejan (zonas de rarefacción), esta alteración de distancias entre las moléculas de aire es lo que produce el sonido. En fluidos altamente incompresibles como los líquidos las distancias se ven muy poco afectadas pero se manifiesta en forma de ondas de presión. La velocidad de propagación de las ondas sonoras en un medio depende de la distancia promedio entre las partículas de dicho medio, por tanto, es en general mayor en los sólidos que en los líquidos y en estos, a su vez, que en los gases. En el vacío no puede propagarse el sonido, nótese que por tanto las explosiones realmente no son audibles en el espacio exterior.
Las ondas sonoras se producen cuando un cuerpo vibra rápidamente. La frecuencia es el número de vibraciones u oscilaciones completas que efectúan por segundo. Los sonidos producidos son audibles por un ser humano promedio si la frecuencia de oscilación está comprendida entre 20 Hz y 20000 Hz. Por encima de esta última frecuencia se tiene un ultrasonido no audible por los seres humanos, aunque algunos animales pueden oír ultrasonidos inaudibles por los seres humanos. La intensidad de un sonido está relacionada con el cuadrado de la amplitud de presión de la onda sonora. Un sonido grave corresponde a onda sonora con frecuencia baja mientras que los sonidos agudos se corresponden con frecuencias más altas.

Compresión esférica (longitudinales) olas.
La física del sonido es estudiada por la acústica, que trata tanto de la propagación de las ondas sonoras en los diferentes tipos de medios continuos como la interacción de estas ondas sonoras con los cuerpos físicos.
onda sinusoidal; Variación de frecuencia; Abajo podemos ver las frecuencias más altas. El eje horizontal representa el tiempo.
|
1. El oído humano percibe sonidos cuyas frecuencias están comprendidas entre 20 y 20000 hertz . Calcular la longitud de onda de los sonidos extremos, si el sonido se propaga en el aire con la velocidad de 330 ms -1.
Al ser l = v/n, las longitudes de onda correspondientes a los sonidos extremos que percibe el oído humano serán, respectivamente:
2. Un foco sonoro colocado bajo el agua tiene una frecuencia de 750 hertz y produce ondas de 2 m. ¿Con qué velocidad se propaga el sonido en el agua?
La velocidad de propagación viene dada por la ecuación:
4. ¿Cuál es el nivel de sensación sonora en decibelios correspondiente a una onda de intensidad 10 -10 W ×m -2? ¿ Y de intensidad 10 -2 W ×m -2? (Intensidad umbral 10 -12 W ×m -2).
Al ser S = 10 log(I/I0) db, resulta:
5. Demostrar que si se duplica la intensidad de un sonido, el nivel de sensación sonora aumenta en 3,0 decibelios.
Tomando como I0 la intensidad inicial, la sensación sonora S0 correspondiente a dicha intensidad I0 es:
y la correspondiente a una intensidad doble:
8. Dos altavoces A y B están alimentados por el mismo amplificador y emiten ondas sinusoidales en fase. El altavoz B está a 2,00 m del altavoz A. La frecuencia de las ondas producidas por los altavoces es 700 Hz y su velocidad en el aire es de 350 m/s. Considerar el punto P entre los altavoces y a lo largo de la línea que los conecta, a una distancia x hacia la derecha del altavoz A. ¿para qué valores de x se producirán interferencias destructivas en el punto P?
La diferencia de caminos para producir interferencias destructivas debe ser: 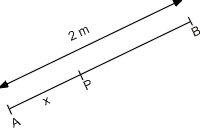
10. Un tubo de órgano abierto en los dos extremos tiene dos armónicos sucesivos con frecuencias de 240 y 280 Hz ¿Cuál es la longitud del tubo?.
La longitud de onda correspondiente a los distintos armónicos, en un tubo con los extremos abiertos, es:.
ln = 2L/n siendo n = 0,1,2,3.0....
La frecuencia de dos armónicos sucesivos es: fn = v·n/2L; fn +1 = v·(n+1)/2L, siendo v la velocidad de propagación
La relación entre las frecuencias 280/240 = n+1/n de donde se deduce que:
28n = 24n + 24 Þ 4n = 24 Þ n = 6
suponiendo que la velocidad del sonido es v = 340 ms-1 la longitud de onda del sexto armónico es: 340/240 = 2L/6 de donde la longitud del tubo es:
L = 4,25 m
|
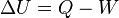 (En termodinámica se considera el trabajo negativo cuando este entra en el sistema termodinámico, positivo cuando sale). Aunque el calor transmitido depende del proceso en cuestión, la variación de energía interna es independiente del proceso, sólo depende del estado inicial y final, por lo que se dice que es una función de estado. Del mismo modo
(En termodinámica se considera el trabajo negativo cuando este entra en el sistema termodinámico, positivo cuando sale). Aunque el calor transmitido depende del proceso en cuestión, la variación de energía interna es independiente del proceso, sólo depende del estado inicial y final, por lo que se dice que es una función de estado. Del mismo modo 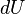 es una diferencial exacta, a diferencia de
es una diferencial exacta, a diferencia de  , que depende del proceso.
, que depende del proceso.  es la diferencia de temperaturas media logarítmica, puede considerarse que el sistema es adiabático cuando se da alguna de las siguientes condiciones:
es la diferencia de temperaturas media logarítmica, puede considerarse que el sistema es adiabático cuando se da alguna de las siguientes condiciones: ), que es la potencia obtenida en el eje, y lapotencia interna ((
), que es la potencia obtenida en el eje, y lapotencia interna (( ), que es la variación por unidad de tiempo de la energía del fluido. La potencia efectiva resulta de restar a la potencia indicada menos la potencia de pérdidas mecánicas (
), que es la variación por unidad de tiempo de la energía del fluido. La potencia efectiva resulta de restar a la potencia indicada menos la potencia de pérdidas mecánicas ( ), que es disipada elrozamiento de elementos mecánicos (cojinetes, retenes, etc.) y en el accionamiento de elementos auxiliares (bomba de aceite, ventiladores, etc.)
), que es disipada elrozamiento de elementos mecánicos (cojinetes, retenes, etc.) y en el accionamiento de elementos auxiliares (bomba de aceite, ventiladores, etc.) ), que es la potencia obtenida en el eje, y lapotencia interna ((
), que es la potencia obtenida en el eje, y lapotencia interna (( ), que es la variación por unidad de tiempo de la energía del fluido. La potencia efectiva resulta de restar a la potencia indicada menos la potencia de pérdidas mecánicas (
), que es la variación por unidad de tiempo de la energía del fluido. La potencia efectiva resulta de restar a la potencia indicada menos la potencia de pérdidas mecánicas ( ), que es disipada elrozamiento de elementos mecánicos (cojinetes, retenes, etc.) y en el accionamiento de elementos auxiliares (bomba de aceite, ventiladores, etc.)
), que es disipada elrozamiento de elementos mecánicos (cojinetes, retenes, etc.) y en el accionamiento de elementos auxiliares (bomba de aceite, ventiladores, etc.)



 . Matemáticamente se dice que dicha función es una onda si verifica la ecuación de ondas:
. Matemáticamente se dice que dicha función es una onda si verifica la ecuación de ondas: es la velocidad de propagación de la perturbación. Por ejemplo, ciertas perturbaciones de la presión de un medio, llamadassonido, verifican la ecuación anterior, aunque algunas ecuaciones no lineales también tienen soluciones ondulatorias, por ejemplo, un solitón.
es la velocidad de propagación de la perturbación. Por ejemplo, ciertas perturbaciones de la presión de un medio, llamadassonido, verifican la ecuación anterior, aunque algunas ecuaciones no lineales también tienen soluciones ondulatorias, por ejemplo, un solitón.










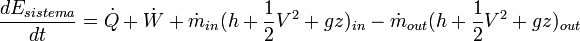





![\dot W = \dot m [(h + \frac{V^{2}}{2})_{out} - (h + \frac{V^{2}}{2})_{in}] = \dot m [ h_{0 out} - h_{0 in} ]](https://upload.wikimedia.org/math/0/4/b/04ba969e4508721476a6c9dd9a6e36c2.png)

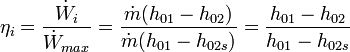
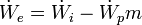



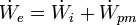




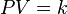
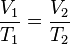 o
o  .
.


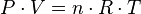

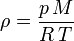
 es la
es la  es la presión del gas,
es la presión del gas,  su
su 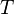 la
la 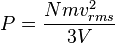 (gas ideal)
(gas ideal)
 ..........(1)
..........(1)

 se puede expresar en función de la presión que se ejerce el gas, y el desplazamiento
se puede expresar en función de la presión que se ejerce el gas, y el desplazamiento 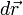 se puede escribir como dx, entonces:
se puede escribir como dx, entonces:
 ..........(2)
..........(2) ..........(3)
..........(3) ..........(4)
..........(4)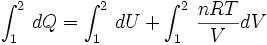
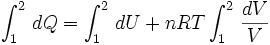
![[Q]_1^2 = [U]_1^2 + nRT[\ln V]_1^2](https://upload.wikimedia.org/math/9/b/b/9bb7def5b45c1c793290a37d2aafc98d.png)
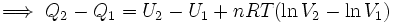
 ..........(5)
..........(5)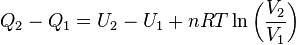


 ,
, =
= 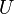 =
= 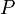 =
=  =
= 

![[Q]_1^2 = [U]_1^2 + P[V]_1^2](https://upload.wikimedia.org/math/1/9/c/19cdd44053e4376e08a03df37aa01416.png)






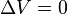 . Esto implica que el proceso no realiza
. Esto implica que el proceso no realiza 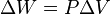 ,
,






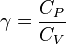
 el
el  el calor específico molar a volumen constante. Para un gas monoatómico ideal,
el calor específico molar a volumen constante. Para un gas monoatómico ideal, 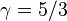 . Para un gas diatómico (como el
. Para un gas diatómico (como el 
 .
.


 ......(1)
......(1) =
= .....(2)
.....(2)




![[P_{2}*V_{2}-P_{1}*V_{1}]/(1-{\gamma})\qquad](https://upload.wikimedia.org/math/1/2/e/12e0bc4e9cc3f701deb42d07a2905b02.png)



 y
y  se relacionan entre sí durante el proceso adiabático. Para ello asumiremos que el sistema es un gas monoatómico, por lo que
se relacionan entre sí durante el proceso adiabático. Para ello asumiremos que el sistema es un gas monoatómico, por lo que
 y
y





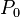 y
y  del estado inicial. Entonces
del estado inicial. Entonces